Float的精度问题

小学故事《小数点的代价》

1967年8月23日，前苏联的联盟一号宇宙飞船在返回大气层时，突然发生了恶性事故–减速降落伞无法打开。

前苏联中央领导研究后决定：向全国实况转播这次事故。当电视台的播音员用沉重的语调宣布，宇宙飞船两个小时后将坠毁，观众将目睹宇航员弗拉迪米-科马洛夫殉难的消息后，举国上下顿时被震撼了，人们沉浸在巨大的悲痛之中。

科马洛夫的女儿也出现在电视屏幕上，她只有12岁。科马洛夫说：”女儿，你不要哭。””我不哭……”女儿已泣不成声，但她强忍悲痛说：”爸爸，您是苏联英雄，我想告诉您，英雄的女儿会像英雄那样生活的！”

科马洛夫叮嘱女儿说：”学习时，要认真对待每一个小数点。联盟一号今天发生的一切，就是因为地面检查时忽略了一个小数点……“

首先，文中的故事，尤其是“小数点”这部分，是儿童文学作家虚构的。

原事故原因极其复杂，有政治因素，也有技术因素，更有大量人为的主观错误。

我们接下来的讨论是基于这个虚构的故事，不要当真。

所以科马洛夫的女儿好好学习认真对待每一个小数点并不能拯救下一个科马洛夫

问题的表象

首先我认为，这个事情不怪地面检查的地勤，一定是俄罗斯程序员的锅 ：）

假定有如下程序：

void func(float a){
  if(a == 3.6f){
    //...执行逻辑:打开火箭返回舱的减速降落伞！
  }
}

if语句代码块中的代码真的可以执行吗？什么情况下可以执行、什么情况下不能执行呢？

再看如下程序：

int a = 0xFFD4194C;//存储减速降落伞的指令编码
float b = (float)a;

这种数据转换真的可以成立吗？变量b中最后存储的还是a中的值吗？

从科马洛夫老哥最后的结局来看，降落伞最终没打开对吧？

这就是经常被提及的浮点数精度问题，接下来我们研究浮点数为什么会有这种反直觉的问题。

Float的存储方式

在以前的文章中，我们讨论过整数数据在内存中的补码存储。

传送门: C语言中的数据存储

但是补码存储，是用来解决减法问题的，并不能解决浮点数存储的问题。

事实上，浮点数存储在内存结构中的数据，与整数型数据完全不同。

IEEE规范的计算方式

目前为止，几乎所有我已知的硬件设备厂商，均遵守IEEE规范设计处理器架构，以支持对浮点数的计算。

当然，也存在因各种原因无法支持IEEE规范，只能通过软件实现该规范的场景，但是那就不在我们的讨论之列了。

存储结构

IEEE规定，对于一个32位数据宽度的单精度浮点数，例如说Float类型变量，有如下存储规范：

最高位	中8位	低23位
0	0000 0000	0000 0000 0000 0000 0000 000
0或1,表示正负符号	存储8位指数	存储23位尾数

可能会感到很奇怪，什么是指数？什么是尾数？

没事，我们接下来简单复习一下小学数学，也就是科马洛夫的女儿需要“好好学习、认真对待”的那部份 ：）

计算方式

以13.5这个浮点数举例，如何计算浮点数存储的位数。

第一步:转换到二进制格式

首先将13.5转换为二进制格式：

整数部份	小数部份
1101	.1000

即二进制小数: 1101.1

第二步:转换为科学计数法表示

接下来将原数转换为科学计数法表示，十进制算术中，我们可以将一万写作: 1 × 10⁴

所以在二进制中，我们也可以把1101.1写作: 1.1011 × 2³

小数点从右至左移动了3位，我们将这个3称之为指数，指数需要存储在中间8位。

第三步:存储符号与指数

还是看这个表格：

最高位	中8位	低23位
0	0000 0000	0000 0000 0000 0000 0000 000

首先，1.1011 × 2³ 是一个正小数，因此可以填入符号位为0。

中间的8位指数位是区分正负的，因此在0~255这256个数里区分了[-128,0)和(0,127] 这两个区间。当我们存储指数3时，需要将3进行坐标平移，即对3进行累加127的操作。3+127 = 128+2, 128即0x80: 1000 0000。所以中8位是 1000 0010 (128 + 2)。

最高位	中8位	低23位
0	1000 0010	0000 0000 0000 0000 0000 000

第四步:存储尾数

1.1011 × 2³ 的指数部份已经存储了，那么接下来存储尾数部份。

由于科学计数法的性质我们可知：整数部份永远是1。所以在存储1.1011时我们可以省略存储整数部份的1，节约1位存储空间，即尾数等于0.1011

对于小数来说，在最低有效位之后补0，不会影响小数的大小，所以尾数填入低23位后，不足填充的部份补0:

最高位	中8位	低23位
0	1000 0010	1011 0000 0000 0000 0000 000

现在我们可以将该数转换为四字节float的16进制表示:

1	2	3	4
0100 0001	0101 1000	0000 0000	0000 0000
41	58	00	00

即0x41580000

float类型的有效存储位其实只有23位，算上偷工减料去掉的整数位上的1，一共是24位。

此时想想看开头的问题，把一个32位长度的四字节整型数据存储进float里，真的可以存储成功吗？

验证

通过 在线浮点转换 验证我们的计算结果:

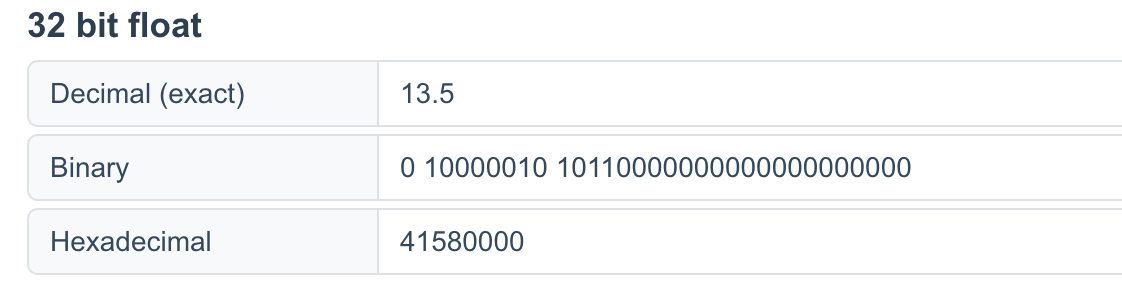
可以看到，计算结果的二进制格式与十六进制格式均与我们计算的一致。

同理可以计算0.625这个浮点的存储格式，与3.5的步骤一致：

转换为二进制小数:

0.625 => 0.101

转换为科学计数法表示:

0.101 => 1.01 × 2⁻¹

指数与尾数:

符号:正小数

指数:-1 (即使是负数，也需要坐标平移127，此处-1+127=126，即0111 1110)

尾数:0.01

最高位	中8位	低23位
0	0111 1110	0100 0000 0000 0000 0000 000

转换为float:

1	2	3	4
0011 1111	0010 0000	0000 0000	0000 0000
3F	20	00	00

即0x3F20000

验证: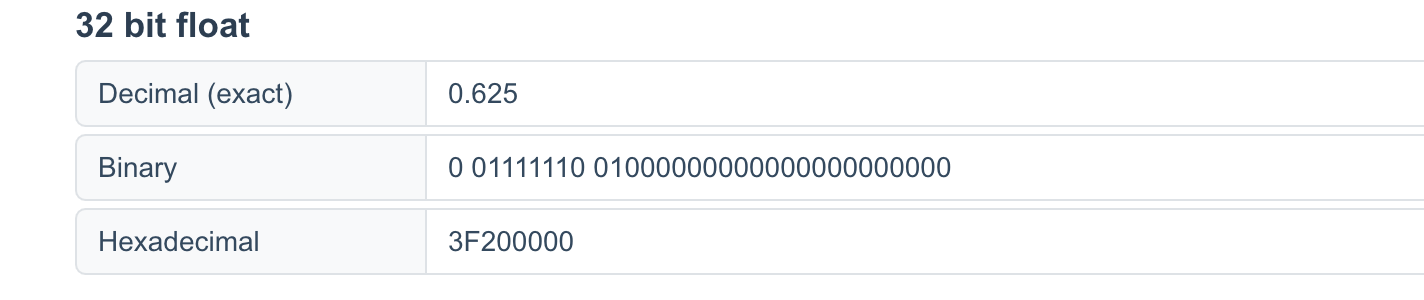

计算结果的二进制格式与十六进制格式均与我们计算的一致。

无法存储的浮点数

当我们尝试存储某些浮点数时，例如0.6。就会发现奇怪的现象，这个浮点数会占满低23位上所有空间。

明明0.6只是个1位十进制小数，为什么需要这么高的精度来存储呢？

十进制小数向二进制转换

当我们尝试将一个10进制小数，例如0.125，转换为二进制小数时，实质上在做如下运算：

计算	结果	整数部份
0.125*2	0.25	0
0.25*2	0.5	0
0.5*2	1.0	1

当计算结果的小数部份为0时，计算终止，按从上到下的顺序写出其整数部份，即为二进制小数，例如0.125就是二进制小数0.001

无法结束的运算

我们尝试用刚刚的方法来计算十进制小数0.6的二进制格式：

计算	结果	整数部份
0.6*2	1.2	1
0.2*2	0.4	0
0.4*2	0.8	0
0.8*2	1.6	1
0.6*2	1.2	1

发现了吗？计算至此，整个计算过程发生了循环，因此该小数在二进制格式下会无限循环：0.100110011001……

因此其float格式内存储的是：

最高位	中8位	低23位
0	0111 1110	0011 0011 0011 0011 0011 010

此处存储空间不足以存下下一个1，所以对最低位进1处理

1	2	3	4
0011 1111	0001 1001	1001 1001	1001 1010
3F	19	99	9A

那么0x3F19999A存储的这个浮点数，其十进制下是什么呢？

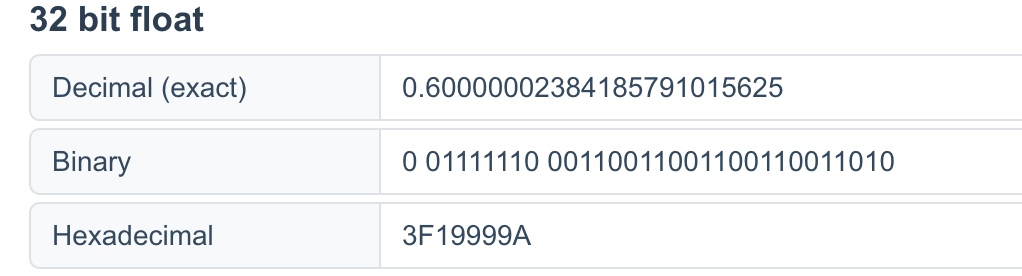
0.60000002384185791015625

由于我们存储该浮点数时，实际上并没有穷尽其尾数，因此这个小数已经不能完全等于原数。

导致在指定精度到小数点后7位之后，该数与原数已经不再相等。

经典问题

现在我们已经明白了，float作为单精度浮点数，受限于IEEE规范的存储格式以及二进制小数的特点，实际上不能穷尽小数的尾数。

因此会发生各种各样的因为浮点数精度导致的BUG。

看我们这段代码：

float a = 0.6f;

float b = 计算加速度系数();// 如果函数返回的是 0.60000002384185791015625f ? :)

if(b > a){
  //执行逻辑:当前情况速度过大，需要打开减速降落伞
  //IEEE:不，你不需要打开
}

此时由于精度问题，就会导致本该执行的代码不被执行。

当然，也可能会导致本不该执行的代码被执行。

这完全取决于代码中指定的计算精度在小数点后几位，如果不指定小数位数，就会发生这类计算BUG。

那么我们如何判断两个浮点数“完全相等”呢？答案是没有办法判断。只能进行“精确到某位小数”下的相等判断，如下形式：

float a = 0.6f;
float b = 计算加速度系数();

//当两数误差精度在小数点后3位以内时，判定相等
if(b - a >= -0.001f && b - a <= 0.001f){
  //执行逻辑,打开减速降落伞
  //科马洛夫:对，我当年就差这一行代码！
}

目前已知所有的高级语言，包括商业机构代码，如微软的高精度计算库，均存在类似问题。

判定小数相等的算法与本文示例原理上并无不同。

所以前苏联程序员要是和哥一样严谨科马洛夫的命就保住了罢